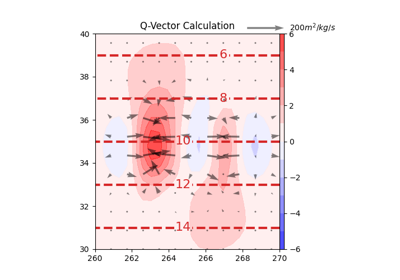
q_vector#
- metpy.calc.q_vector(u, v, temperature, pressure, dx=None, dy=None, static_stability=1, x_dim=-1, y_dim=-2, *, parallel_scale=None, meridional_scale=None, latitude=None, longitude=None, crs=None)[source]#
Calculate Q-vector at a given pressure level using the u, v winds and temperature.
\[\vec{Q} = (Q_1, Q_2) = - \frac{R}{\sigma p}\left( \frac{\partial \vec{v}_g}{\partial x} \cdot \nabla_p T, \frac{\partial \vec{v}_g}{\partial y} \cdot \nabla_p T \right)\]This formula follows equation 5.7.55 from [Bluestein1992], and can be used with the the below form of the quasigeostrophic omega equation to assess vertical motion ([Bluestein1992] equation 5.7.54):
\[\left( \nabla_p^2 + \frac{f_0^2}{\sigma} \frac{\partial^2}{\partial p^2} \right) \omega = - 2 \nabla_p \cdot \vec{Q} - \frac{R}{\sigma p} \beta \frac{\partial T}{\partial x}\]By default, this function uses a unitless value of 1 for
static_stability, which replicates the functionality of the GEMPAKQVECfunction. If a value is given forstatic_stability, it should have dimensionality ofenergy / mass / pressure^2, and will result in behavior that matches that of GEMPAK’sQVCLfunction;static_stabilitycan be used to calculate this value if desired.- Parameters:
u ((…, M, N)
xarray.DataArrayorpint.Quantity) – x component of the wind (geostrophic in QG-theory)v ((…, M, N)
xarray.DataArrayorpint.Quantity) – y component of the wind (geostrophic in QG-theory)temperature ((…, M, N)
xarray.DataArrayorpint.Quantity) – Array of temperature at pressure levelpressure (
pint.Quantity) – Pressure at leveldx (
pint.Quantity, optional) – The grid spacing(s) in the x-direction. If an array, there should be one item less than the size of u along the applicable axis. Optional ifxarray.DataArraywith latitude/longitude coordinates used as input.dy (
pint.Quantity, optional) – The grid spacing(s) in the y-direction. If an array, there should be one item less than the size of u along the applicable axis. Optional ifxarray.DataArraywith latitude/longitude coordinates used as input.static_stability (
pint.Quantity, optional) – The static stability at the pressure level. Defaults to 1 if not given to calculate the Q-vector without factoring in static stability.x_dim (int, optional) – Axis number of x dimension. Defaults to -1 (implying […, Y, X] order). Automatically parsed from input if using
xarray.DataArray.y_dim (int, optional) – Axis number of y dimension. Defaults to -2 (implying […, Y, X] order). Automatically parsed from input if using
xarray.DataArray.parallel_scale (
pint.Quantity, optional) – Parallel scale of map projection at data coordinate. Optional ifxarray.DataArraywith latitude/longitude coordinates and MetPy CRS used as input. Also optional if longitude, latitude, and crs are given. If otherwise omitted, calculation will be carried out on a Cartesian, rather than geospatial, grid. Keyword-only argument.meridional_scale (
pint.Quantity, optional) – Meridional scale of map projection at data coordinate. Optional ifxarray.DataArraywith latitude/longitude coordinates and MetPy CRS used as input. Also optional if longitude, latitude, and crs are given. If otherwise omitted, calculation will be carried out on a Cartesian, rather than geospatial, grid. Keyword-only argument.latitude (
pint.Quantity, optional) – Latitude of data. Optional ifxarray.DataArraywith latitude/longitude coordinates used as input. Also optional if parallel_scale and meridional_scale are given. If otherwise omitted, calculation will be carried out on a Cartesian, rather than geospatial, grid. Keyword-only argument.longitude (
pint.Quantity, optional) – Longitude of data. Optional ifxarray.DataArraywith latitude/longitude coordinates used as input. Also optional if parallel_scale and meridional_scale are given. If otherwise omitted, calculation will be carried out on a Cartesian, rather than geospatial, grid. Keyword-only argument.crs (
pyproj.crs.CRS, optional) – Coordinate Reference System of data. Optional ifxarray.DataArraywith MetPy CRS used as input. Also optional if parallel_scale and meridional_scale are given. If otherwise omitted, calculation will be carried out on a Cartesian, rather than geospatial, grid. Keyword-only argument.
- Returns:
tuple of (…, M, N)
xarray.DataArrayorpint.Quantity– The components of the Q-vector in the u- and v-directions respectively
Changed in version 1.0: Changed signature from
(u, v, temperature, pressure, dx, dy, static_stability=1)See also