Sigma to Pressure Interpolation

By using metpy.calc.log_interp, data with sigma as the vertical coordinate can be interpolated to isobaric coordinates.

import cartopy.crs as ccrs
import cartopy.feature as cfeature
import matplotlib.pyplot as plt
from netCDF4 import Dataset, num2date

import metpy.calc as mcalc
from metpy.cbook import get_test_data
from metpy.plots import add_metpy_logo
from metpy.units import units

Data

The data for this example comes from the outer domain of a WRF-ARW model forecast initialized at 1200 UTC on 03 June 1980. Model data courtesy Matthew Wilson, Valparaiso University Department of Geography and Meteorology.

data = Dataset(get_test_data('wrf_example.nc', False))
lat = data.variables['lat'][:]
lon = data.variables['lon'][:]
time = data.variables['time']
vtimes = num2date(time[:], time.units)
temperature = data.variables['temperature'][:] * units(data.variables['temperature'].units)
pres = data.variables['pressure'][:] * units(data.variables['pressure'].units)
hgt = data.variables['height'][:] * units(data.variables['height'].units)

Array of desired pressure levels

plevs = [700.] * units.hPa

Interpolate The Data

Now that the data is ready, we can interpolate to the new isobaric levels. The data is interpolated from the irregular pressure values for each sigma level to the new input mandatory isobaric levels. mcalc.log_interp will interpolate over a specified dimension with the axis argument. In this case, axis=1 will correspond to interpolation on the vertical axis.

isobaric_levels = mcalc.log_interp(plevs, pres, hgt, temperature, axis=1)

The interpolated data is output in a list, so we will pull out each variable for plotting.

height = isobaric_levels[0]
temp = isobaric_levels[1]

Plotting the Data for 700 hPa.

# Set up our projection
crs = ccrs.LambertConformal(central_longitude=-100.0, central_latitude=45.0)

# Set up our array of latitude and longitude values and transform to
# the desired projection.
tlatlons = crs.transform_points(ccrs.PlateCarree(), lon, lat)
tlons = tlatlons[:, :, 0]
tlats = tlatlons[:, :, 1]

# Get data to plot state and province boundaries
states_provinces = cfeature.NaturalEarthFeature(category='cultural',
                                                name='admin_1_states_provinces_lakes',
                                                scale='50m',
                                                facecolor='none')

# Set the forecast hour
FH = 1

# Create the figure and grid for subplots
fig = plt.figure(figsize=(17, 12))
add_metpy_logo(fig, 470, 320, size='large')

# Plot 700 hPa
ax = plt.subplot(111, projection=crs)
ax.coastlines('50m', edgecolor='black', linewidth=0.75)
ax.add_feature(states_provinces, edgecolor='black', linewidth=0.5)

# Plot the heights
cs = ax.contour(tlons, tlats, height[FH, 0, :, :],
                colors='k', linewidths=1.0, linestyles='solid')
plt.clabel(cs, fontsize=10, inline=1, inline_spacing=7,
           fmt='%i', rightside_up=True, use_clabeltext=True)

# Contour the temperature
cf = ax.contourf(tlons, tlats, temp[FH, 0, :, :], range(-20, 20, 1), cmap=plt.cm.jet)
cb = plt.colorbar(cf, orientation='horizontal', extend=max, aspect=65, shrink=0.5, pad=0.05,
                  extendrect='True')
cb.set_label('Celsius', size='x-large')

ax.set_extent([-106.5, -90.4, 34.5, 46.75], crs=ccrs.PlateCarree())

# Make the axis title
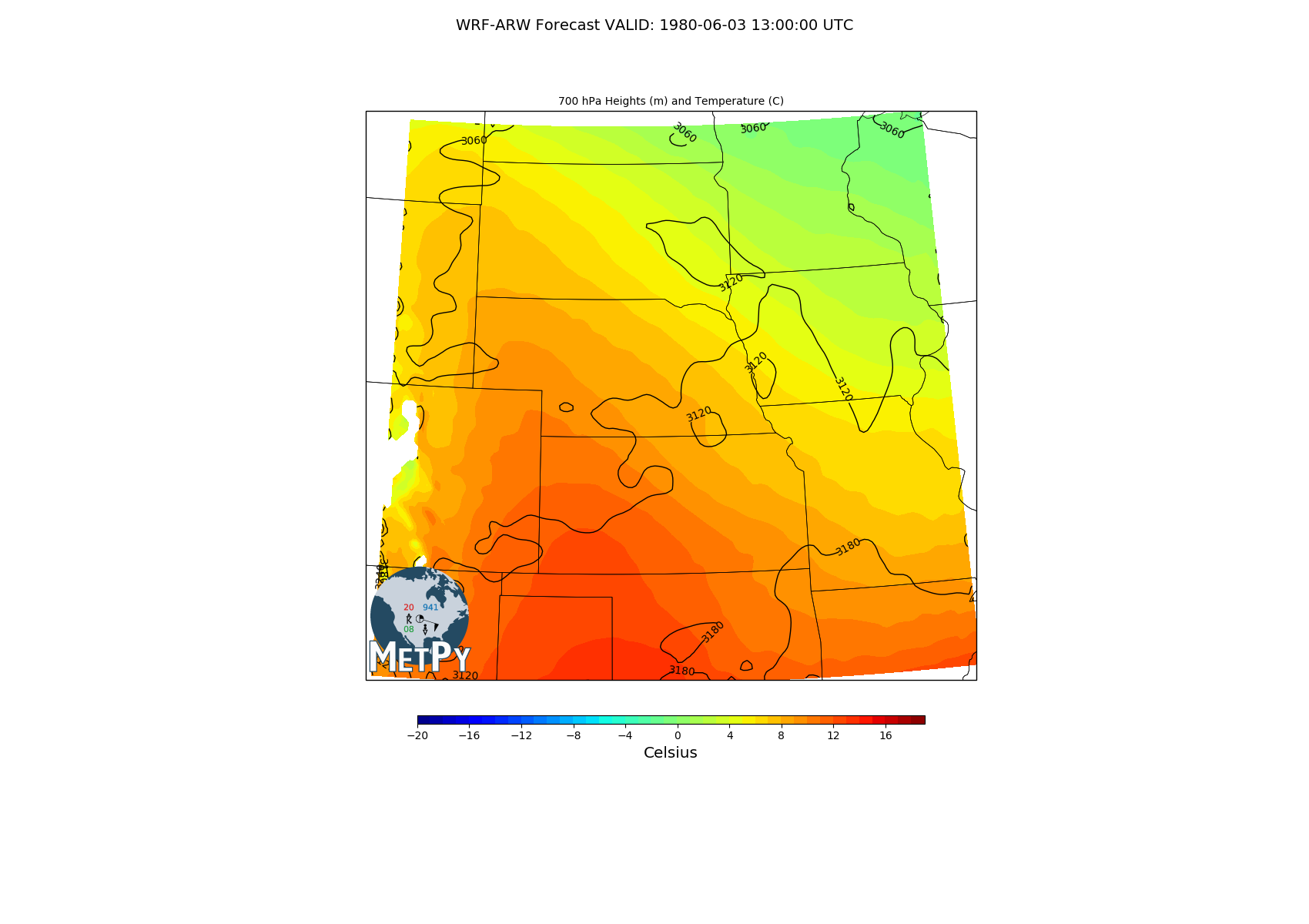
ax.set_title('{:.0f} hPa Heights (m) and Temperature (C)'.format(plevs[0].m), loc='center',
             fontsize=10)

# Set the figure title
fig.suptitle('WRF-ARW Forecast VALID: {:s} UTC'.format(str(vtimes[FH])), fontsize=14)
plt.show()

Total running time of the script: ( 0 minutes 1.977 seconds)